Elimination method is used to solve the linear equation in two variables, where one of the variables is eliminated This method is sometimes easier and convenient than the substitution methodSimple and best practice solution for (x1)2(y3)2=9 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework Simplify (x− 1 2y4)1 4 x2 3y3 2x−3 2y1 2 First, let's distribute the 1 4 exponent x( − 1 2)1 4 y(4)1 4 x2 3y3 2x− 3 2y1 2 When you raise a power to a power you multiply them to find the exponent Let's do that x( − 1 2)( 1 4)y(4) (1 4) x2 3y3 2x− 3 2y1 2 x− 1 8y1 x2 3y3 2x− 3 2y1 2 x− 1 8y x2 3y3 2x− 3 2y1 2

Ex 3 6 1 I And Ii Solve 1 2x 1 3y 2 1 3x 1 2y
X 1/2 y-1/3=8 x-1/3 y 1/2=9 by elimination method
X 1/2 y-1/3=8 x-1/3 y 1/2=9 by elimination method- Solution The system is readily obtained as below x 3 y − 5 z = 2 2 x − 3 z = − 5 3 x 2 y − 3 z = − 1 Once a system is expressed as an augmented matrix, the GaussJordan method reduces the system into a series of equivalent systems by using the row operations This row reduction continues until the system is expressed in what isOr click the example About Elimination Use elimination when you are solving a system of equations and you can quickly eliminate one variable by adding or




Solve For X And Y 1 2 2x 3y 12 7 3x 2y 7 2x 3y 4 3x 2y 2 For 2x 3y 0 And 3x 2y 0 Brainly In
The equation is in standard form 6y=3x 6 y = − 3 x Divide both sides by 6 Divide both sides by 6 \frac {6y} {6}=\frac {3x} {6} 6 6 y = − 6 3 x Dividing by 6 undoes the multiplication by 6 Dividing by 6 undoes the multiplication by 6Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyStep 1 Multiply one, or both, of the equations to set up the elimination of one of the variables In this example, we will eliminate the variable y by multiplying both sides of the first equation by 2 Take care to distribute This leaves us with an equivalent system where the variable y
X/22y/3=1 and xy/3=3 solve by elimination method Get the answers you need, now!Add 2 2 and 3 3 Move x1 4 x 1 4 to the numerator using the negative exponent rule 1 bn = b−n 1 b n = b n Multiply x1 2 x 1 2 by x−1 4 x 1 4 by adding the exponents Tap for more steps Use the power rule a m a n = a m n a m a n = a m n to combine exponentsClick here👆to get an answer to your question ️ Solve the following system of equations by using Matrix inversion method 2x y 3z = 9,x y z = 6,x y z = 2
Simple and best practice solution for 2(x3)9=3(x1)x equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homeworkQuestion 4253 xy=1 xy=3 The instructions say "Use elimination to solve each system of equations" I have absolutely no clue what to do I think you're supposed to11x8y=6 Geometric figure Straight Line Slope = 2750/00 = 1375 xintercept = 6/11 = yintercept = 6/8 = 3/4 = Rearrange Rearrange the equation by




Solving A System Of Equations Using A Matrix Precalculus Socratic




Linear Equations Questions And Answers Topperlearning
Example 18 Solve the following pair of equations by reducing them to a pair of linear equations 5/(𝑥 −1) 1/(𝑦 −2) = 2 6/(𝑥 −1) – 3/(𝑦 −2) = 1 5/(𝑥 − 1) 1/(𝑦 − 2) = 2 6/(𝑥 − 1) – 3/(𝑦 − 2) = 1 So, our equations become 5u v = 2 6u – 3v = 1 Thus, our Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queries Students (upto class 102) preparing for All Government Exams, CBSE Board Exam, ICSE Board Exam, State Board Exam, JEE (MainsAdvance) and NEET can ask questions from any subject and get quick answers byAnswer to If y= 1 X 8 X 8 (x 2)3(x27) (3x 1)2(x 8)



Q Tbn And9gcrd6h17gerq Uh9n8oen0yturw2395ogtdwdnzlspnl7qcxkcye Usqp Cau




Ex 3 6 1 I And Ii Solve 1 2x 1 3y 2 1 3x 1 2y
Click here👆to get an answer to your question ️ Solve the following pairs of linear equation by the elimination method and the substitution method(i) 3x 5y 4 = 0 and 9x = 2y 7 (ii) x2 2y3 = 1 and xAnswer to 1 (22) Calculate the change in x, change of y & rate of change for the line provided = n 5 OC (m) = 5 O C(m) = (5) OC" (m) = m 5 15 (3x4y=17 (2x5y = 2 Which method would be best to solve this sytem?* (2 points) Substitution We have an isolated variable in one equation ready to substitute into the other equation 1/2 x (6 2/7 x) = 5 11/14 x = 11 x = 14 or, you can use elimination since 1/3 = 2/6, 2/7 x 1/3 y = 6 1/2 x 1/3 y = 5 Now add the two equations to get rid of the y 11/14 x = 11




Solve X 1 2 Y 1 3 8 X 1 3 Y 1 2 9 Youtube




Step By Step Math Wolfram Alpha Blog
This set of Numerical Analysis Multiple Choice Questions & Answers (MCQs) focuses on "Gauss Elimination Method – 1" 1 Solve the following equations by Gauss Elimination Method Hence, x = 2 Find the values of x, y, z in the following system of equations by gauss Elimination Method z = 6 Hence y = 4The elimination method of solving systems of equations is also called the addition method To solve a system of equations by elimination we transform the system such that one variable "cancels out" Example 1 Solve the system of equations by elimination $$ \begin{aligned} 3x y &= 5 \\ x y &= 3 \end{aligned} $$ x 1 2 y 1 3 8 x 1 3 y 1 2 9 Mathematics TopperLearningcom hye7rgtt Starting early can help you score better!



Q Tbn And9gcqxnk Lpfjle Erogd0wsraw D67yjyrnkghuofquiwt4u Rzfp Usqp Cau




Solve For X And Y X 1 2 Y 1 3 9 And X 1 3 Y 1 2 8 Brainly In
A (x – 2)2/25 (y 1)2/9 = 1 B (x – 2)2/24 (y 1)2/36 = 1 C (x – 2)2/35 (y 1)2/25 = 1 D (x – 2)2/22 (y 1)2/50 = 1 Question 29 of 40 Convert each equation to standard form by completing the square on x and y 4×2 y2 16x – 6y – 39 = 0 A (x 2)2/4 (y – 3)2/39 = 1 B (x 2)2/39 (y – 4)2/64 = 1Therefore, x = – 8 and y = – 4 2 (i) ¾ x – 2/3 y = 1 3/8 x – 1/6 y = 1 (ii) 2x – 3y – 3 = 0 2x/3 4y ½ = 0 Solution (i) ¾ x – 2/3 y = 1 3/8 x – 1/6 y = 1 We can write it as ¾ x – 2/3 y = 1 (9x – 8y)/ 12 = 1 By cross multiplication 9x – 8y = 12 (1) 3/8 x – 1/6 y = 1 (9x – 4y)/ 24 = 1 By crossStep by step solution of a set of 2, 3 or 4 Linear Equations using the Substitution Method x/8y/2=1;x/3y=2 Tiger Algebra Solver




X 1 2 Y 1 3 8 X 1 3 Y 1 2 9



Http Www Math Utep Edu Faculty Cmmundy Math 2301 Solution Manual Pdf
Answer to Solve by the elimination method 3x y = 1;Step1 Multiply the coefficient of the first term by the constant 1 • 5 = 5 Step2 Find two factors of 5 whose sum equals the coefficient of the middle term, which is 6 5 1 = 6 That's it Step3 Rewrite the polynomial splitting the middle term using the two factors found in step 2 above, 5 and 1X 8y = 42 By signing up, you'll get thousands of stepbystep solutions to your homework




Solve 3 X Y 2 X Y 2 And 9 X Y



Home Hvl No Ansatte Tct Ftp V hydrodynamikk Matlab Ch06ny Eksempler Pdf
Assuming inverse variation between x and y means y = k/x in this context, (y3) = k/(x4) Plugging in x=8 and y=2, we get 5 = k/4, or k = Plugging in y=1 and k=, we get 2 = /(x4) Simplified as (x4) = 10 Simplified as x = 14 Edit did opAvail 25% off on study pack Avail OfferSolution of linear system by Gaussian elimination method 1) Apply Gauss elimination method to find the solution of the following system x 4 6 8 10 y 1 3 8 16 3) Find the value of y at x 21 and x 28 Use Romberg's method to compute 1 2 0 1 dx ³ x correct to 4 decimal places Also evaluate




Ex 3 6 1 I And Ii Solve 1 2x 1 3y 2 1 3x 1 2y
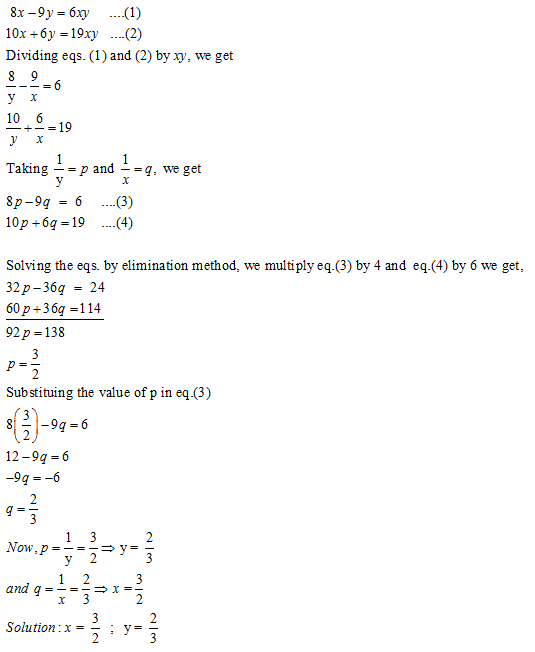



Solve X And Y A 8x 9y 6xy 10x 6y 19xy B X Y 2 Y 1 3 8 X 1 3 Y 1 2 9 Mathematics Topperlearning Com 4xcbunxx
Solve the Given equation in Elimination method and Substitution MethodQuestion 1 Solve the following systems of linear equations by Gaussian elimination method 2x − 2y 3z = 2, x 2y − z = 3, 3x − y 2z = 1 We need to calculate the value of x and y Using equation (III) and (IV) Solving by elimination method Multiply by 2 of equation (III) and multiply by 3 of equation (IV) After solving Put the value of y in equation (I) Hence, The value of x and y is and



Substitution Method Review Systems Of Equations Article Khan Academy




Ylay52vmlzsj7m
A Fixed point iteration method for solving equation f(x) = 0 Procedure (1 Sin x)1/3 = h 1 (x) and x = Sin1(x3 1)= h 2 (x) We see that I h (x) = y 0 p Δ y 0 p(p – 1)/2 cocept of elimation method The sum of the digits of a two digit number is 12 The number obtained by interchanging Its digits exceed the given number by 18 find the number pxqy=pq qxpy=pq x2y=5 3x/23y=10 solve by elimination method(a) 2x 3y = 12(i) and x y = 1(ii) (ii)×3 ==> 3x 3y = 3(iii) Now we can eliminate y by adding (i) & (iii) (i) (iii) ==> 5x = 15 so x=3




Ex 3 4 1 Solve By Elimination And Substitution I X Y 5 2x 3y




Ylay52vmlzsj7m
Solutions to Systems of Linear Equations¶ Consider a system of linear equations in matrix form, \(Ax=y\), where \(A\) is an \(m \times n\) matrix Recall that this means there are \(m\) equations and \(n\) unknowns in our system A solution to a system of linear equations is an \(x\) in \({\mathbb{R}}^n\) that satisfies the matrix form equation Depending on the values that populate To eliminate the y value, add the equations (1) and (2) Divide to each side by 11 Substitute the x value in (1) Subtract 15 from each side Divide to each side by nagitive 4 Solution x = 5, ySECTION 51 GAUSSIAN ELIMINATION matrix form of a system of equations The system 2x3y4z=1 5x6y7z=2 can be written as Ax ó =b ó where A= 234 567,x ó = x y z,b ó = 1 2 The system is abbreviated by writing (1) 234 567 1 2 The matrix A is called the coefficient matrixThe2Å4 matrix in (1) is called the augmented matrix and is



Step By Step Math Wolfram Alpha Blog



Chapter 1
Solve by Addition/Elimination xy=1 xy=3 Multiply each equation by the value that makes the coefficients of opposite Simplify Tap for more steps Simplify Tap for more steps Apply the distributive property Rewrite as MultiplyAsked in ALGEBRA 1 by futai Scholar reshown by goushi Share this question Substitute the value of x in (1) 2*15y = 3230y = 32 Add 30 to each side3030y = 3230y =62 Multiple to each side by negitive one y = 62 Solution is x =15, y = 62Solve the following systems of equations x y z = 4 x 2y 3z = 9 2x y 3z = 1 asked Apr 26 in Linear Equations by Haifa ( k points) pair of linear equations in two variables




Amc Solutions Manual Glenco Solution




Express A Vector As A Linear Combination Of Other Vectors Problems In Mathematics
Solve the following systems of linear equations by Gaussian elimination method (i) 2x – 2y 3z = 2, x 2y – z = 3, 3x – y 2z = 1 (ii) 2x 4y 6z = 22, 3x 8y 5z = 27, x y 2z = 2 Solution (i) 2x – 2y 3z = 2, x 2y – z = 3 and 3x – y 2z = 1X^2y^2=9 WolframAlpha Volume of a cylinder?Piece of cake Unlock StepbyStep x^2y^2=9 Extended Keyboard Examples




3z D7ceexznd9m
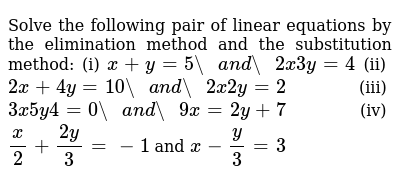



Solve The Following Pair Of Linear Equations By The Elimination M
x=3, y=5 Subtracting equations, x 2x = 2 1 x = 3 x = 3 y = 2 x= 2 3 = 5 Check 3 5 = 2 quad sqrt 2(3) 5 = 1 quad sqrt Transcript Ex 36, 1 Solve the following pairs of equations by reducing them to a pair of linear equations (i) 1/2𝑥 1/3𝑦 = 2 1/3𝑥 1/2𝑦 = 13/6 1/2𝑥 1/3𝑦 = 2 1/3𝑥 1/2𝑦 = 13/6 Let 1/𝑥 = u 1/𝑦 = v So, our equations become 1/2 u 1/3 v = 2 (3𝑢 2𝑣)/(2 × 3) = 2 3u 2v = 12 1/3 u 1/2 v = 13/6 (2𝑢 3𝑣)/(2 × 3) = 13/6 2u 3v = 13 Our equationsQuestion Need help solving system by elimination method x/2 y/3 = 7/6 2x/3 3y/4 = 5/4 Thank you Found 3 solutions by Alan3354, Fombitz, rothauserc




Step By Step Math Wolfram Alpha Blog




Ml Aggarwal Solutions For Class 9 Maths Chapter 5 Simultaneous Linear Equations
Solving a System of Linear Equations Using Matrices We have seen how to write a system of equations with an augmented matrix, and then how to use row operations and backsubstitution to obtain rowechelon form Now, we will take rowechelon form a step farther to solve a 3 by 3 system of linear equations The general idea is to eliminate allXy=5;x2y=7 Try it now Enter your equations separated by a comma in the box, and press Calculate! Pair of Linear Equations in Two Variables Solve for x and y x1/2 y1/3=8, x1/3y1/2=9 Share with your friends




Ex 3 6 1 I And Ii Solve 1 2x 1 3y 2 1 3x 1 2y



Pdf Introduction To Differential Equations Exercises 1 1 상민 손 Academia Edu




Ex 3 3 1 Solve By Substitution Method I X Y 14 Ex 3 3




X 1 2 Y 1 3 8 X 1 3 Y 1 2 9 Simultaneous Linear Equation Brainly In




7 Proof By Induction 1 3 5 7 2n 1 N 2 Discrete Prove All N In N Induccion Mathgotserved Youtube




Solve The Equations Using Elimination Method 5x 6y 9 And X Y 4




Algebra 2 Solutions Pdf Integer Rational Number



Http Www Math Utep Edu Faculty Cmmundy Math 2301 Solution Manual Pdf




Sum And Product Notation Karnaugh Mapping Electronics Textbook



Distance Between Point Line Video Khan Academy




Solve For X And Y 1 2 2x 3y 12 7 3x 2y 7 2x 3y 4 3x 2y 2 For 2x 3y 0 And 3x 2y 0 Brainly In




Sum And Product Notation Karnaugh Mapping Electronics Textbook




Ex 3 4 1 Solve By Elimination And Substitution I X Y 5 2x 3y




Ex 3 3 1 Solve By Substitution Method I X Y 14 Ex 3 3



Http Www Math Utep Edu Faculty Cmmundy Math 2301 Solution Manual Pdf




Ex 3 3 1 Solve By Substitution Method I X Y 14 Ex 3 3



Step By Step Math Wolfram Alpha Blog




X 1 2 Y 1 3 8 X 1 3 Y 1 2 9



Math Questions Math Answers
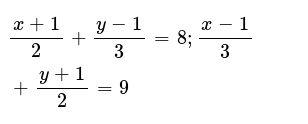



Solve For X And Y X 1 2 Y 1 3 9 X 1 3 Y 1 2 8



Distance Between Point Line Video Khan Academy



Python Challenges 1 Exercises Practice Solution W3resource




Solving A System Of Equations Using A Matrix Precalculus Socratic




Pdf Soluciones Matematicas Para Administracion Y Economia De Hausseler Vicente Amezola Academia Edu
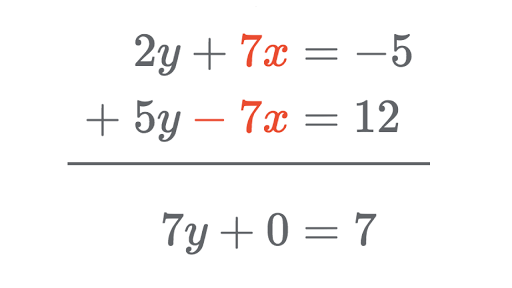



Elimination Method Review Systems Of Linear Equations Article Khan Academy



Did You Solve It Are You Smarter Than A Singaporean Ten Year Old Mathematics The Guardian




Step By Step Math Wolfram Alpha Blog
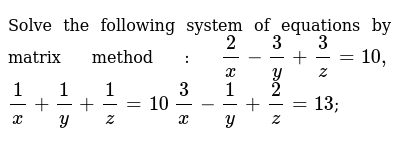



Solve The Following System Of Equations By Matrix Method




Ex 3 6 1 I And Ii Solve 1 2x 1 3y 2 1 3x 1 2y



Www Casdschools Org Cms Lib Pa Centricity Domain 904 practice 9 Pdf




Did You Solve It Are You Smarter Than A Singaporean Ten Year Old Mathematics The Guardian




Selected Answers New Lexington City Schools



Search Q X 7 2by 3 3d5 X 2 Y 9 3d6 By Elimination Method Tbm Isch




Solve For X And Y X 1 2 Y 1 3 9 And X 1 3 Y 1 2 8 Brainly In




Ex 3 6 1 I And Ii Solve 1 2x 1 3y 2 1 3x 1 2y




If X 2 1 X 2 34 Find X 3 1 X 3 Most Important Question In Algebra Youtube




Ex 3 3 1 Solve By Substitution Method I X Y 14 Ex 3 3




Solving A System Of Equations Using A Matrix Precalculus Socratic




Solve The Following Pair Of Linear Equations By Substitution Method 2x 3y 19 And 3x 2y 21



Solve For X And Y X 1 2 Y 1 3 9 X 1 3 Y 1 2 8 Sarthaks Econnect Largest Online Education Community




Chapter 1




New Syllabus Mathematics 2




3z D7ceexznd9m



Www Cimt Org Uk Projects Mepres Step Up Mepanswers Pdf



Http Www Math Utep Edu Faculty Cmmundy Math 2301 Solution Manual Pdf




Nm Tutorial Problems



Solve For X And Y X 1 2 Y 1 3 9 X 1 3 Y 1 2 8 Sarthaks Econnect Largest Online Education Community




Solve The Following Pair Of Linear Equation By The Substitution Method 2x Y 1 4x 3y 27 Brainly In



Linear Equations Questions And Answers Topperlearning




Ex 3 6 1 I And Ii Solve 1 2x 1 3y 2 1 3x 1 2y




Solve X 1 2 Y 1 3 8 X 1 3 Y 1 2 9 Youtube




X 1 2 Y 1 3 8 X 1 3 Y 1 2 9
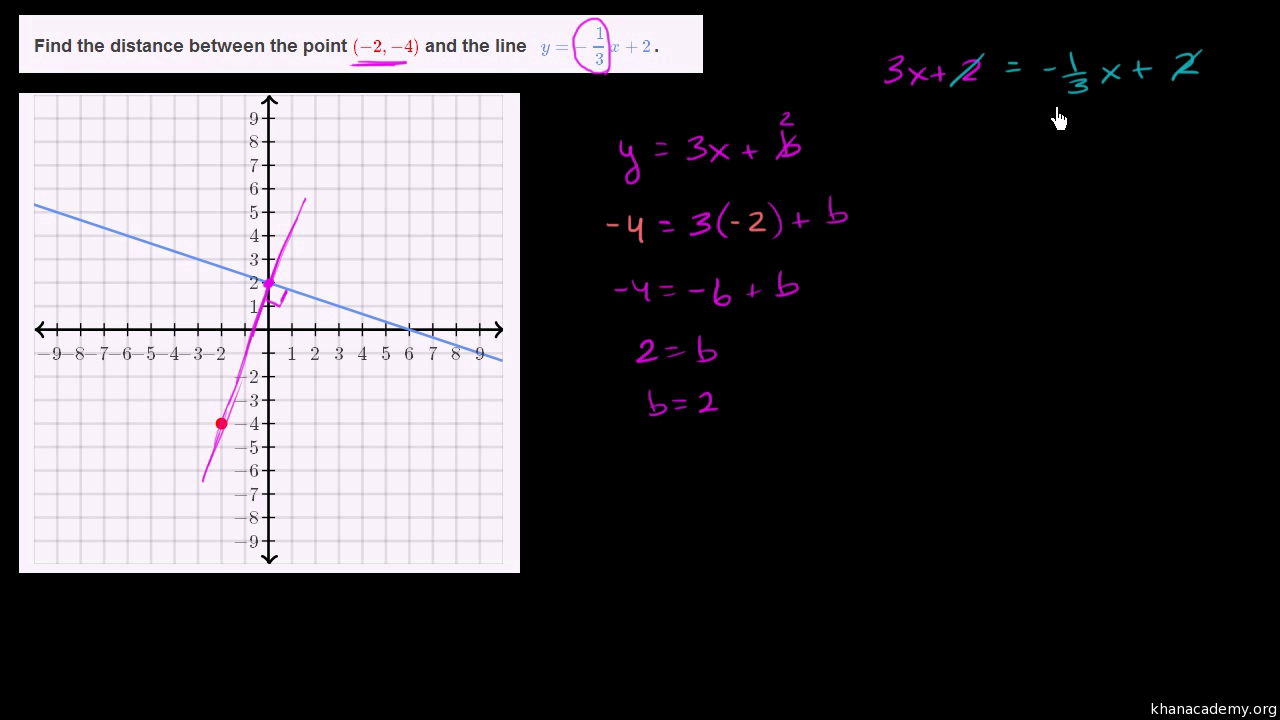



Distance Between Point Line Video Khan Academy
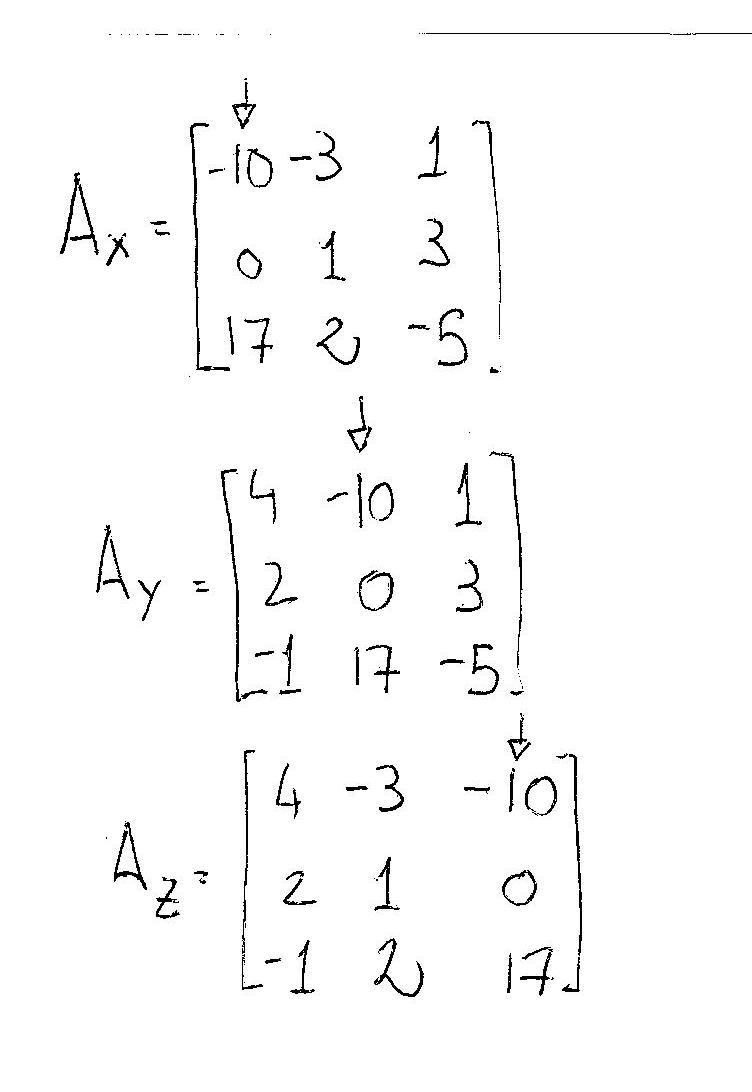



Solving A System Of Equations Using A Matrix Precalculus Socratic




Algebra 2 Solutions Pdf Integer Rational Number




Ylay52vmlzsj7m




Mathematics For Academic Studies 4 Student S Book Sample By Grupo Anaya S A Issuu




Solve The Following Pair Of Linear Equations By The Elimination M




Solve 2 2x 1 X 3 3 X 3 2x 1 5 e 3 1 2 Youtube




Solve The Following Pair Of Linear Equations By The Elimination M




Brief Calculus With Integrated Precalculus By




X 1 2 Y 1 3 8 X 1 3 Y 1 2 9 Simultaneous Linear Equation Brainly In




Solve X 1 2 Y 1 3 8 X 1 3 Y 1 2 9 Youtube




Ylay52vmlzsj7m




Ex 3 6 1 I And Ii Solve 1 2x 1 3y 2 1 3x 1 2y



Solving A System Of Equations Using A Matrix Precalculus Socratic



Q Tbn And9gcqfrqxr507ozco1lhgiqwot Cdchophjbocrnsjhblpnw2oyhom Usqp Cau




Step By Step Math Wolfram Alpha Blog




X 1 2 Y 1 3 8 X 1 3 Y 1 2 9 Simultaneous Linear Equation Brainly In




Ylay52vmlzsj7m




Using Gauss Jordan To Solve A System Of Three Linear Equations Example 1 Youtube
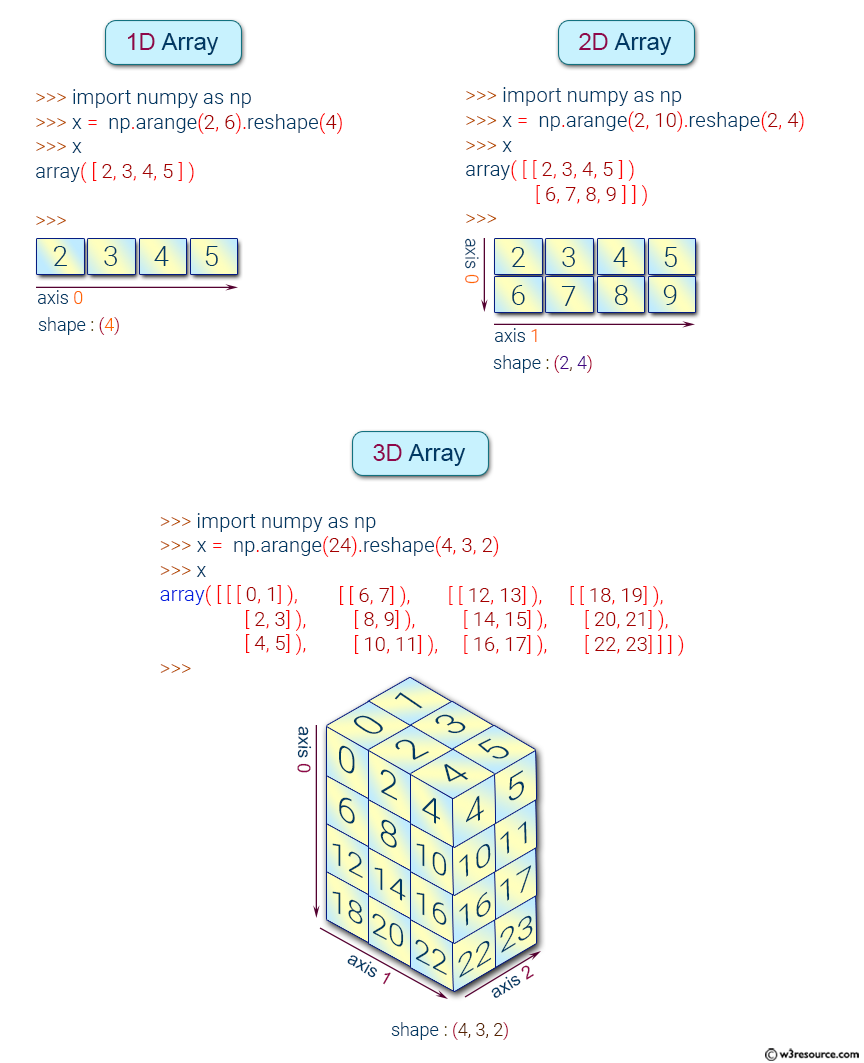



Numpy Array Object Exercises Practice Solution W3resource
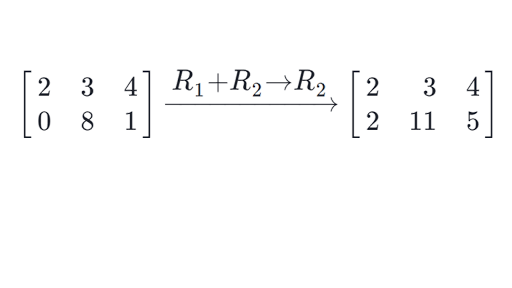



Matrix Row Operations Article Matrices Khan Academy




Line Of Best Fit Least Square Method




Brief Calculus With Integrated Precalculus By




Solve For X 1 2x Upon X 3 1 Upon 2x 3 3x 9upon X 3 2x 3 0 X Is Not Equal To The 3 Minus 3 Upon 2 Brainly In



Web Iit Edu Sites Web Files Departments Academic Affairs Academic Resource Center Pdfs Kmaps Pdf
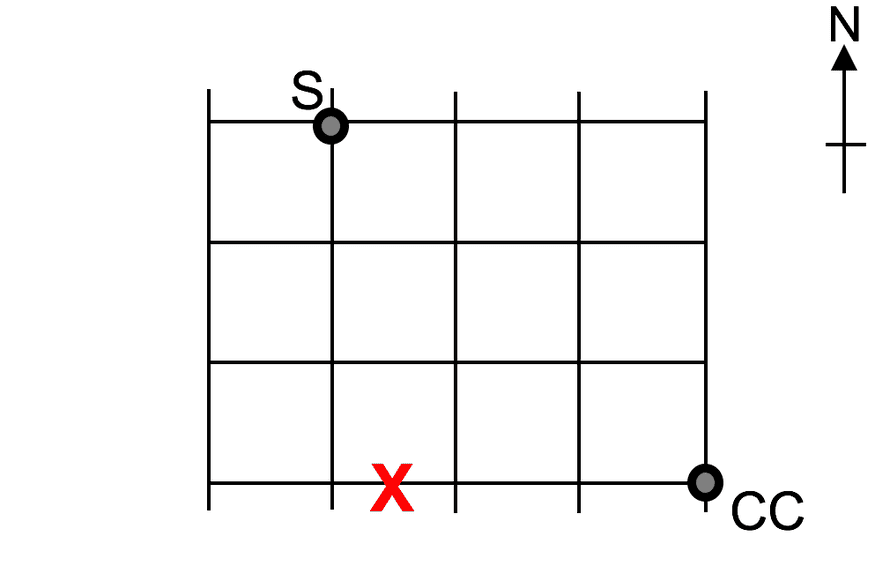



Did You Solve It Are You Smarter Than A Singaporean Ten Year Old Mathematics The Guardian



0 件のコメント:
コメントを投稿